En esta sección serán definidas las Razones Trigonométricas para un triángulo rectángulo, se calcularán algunos Valores ilustres que serán utilizados muy frecuentemente y se mostrarán Ejemplos de Aplicación a situaciones problemáticas.
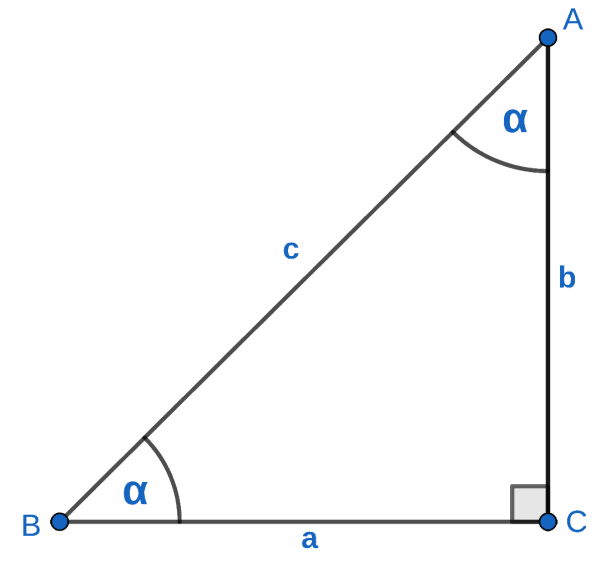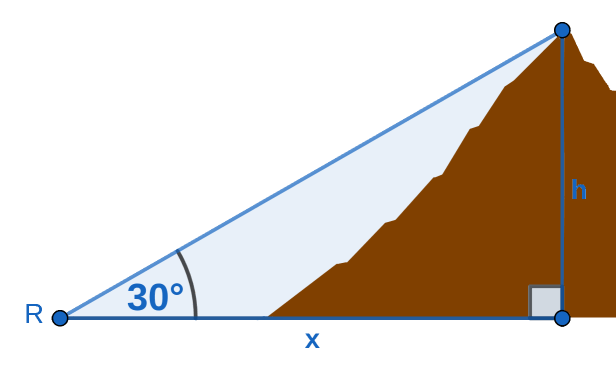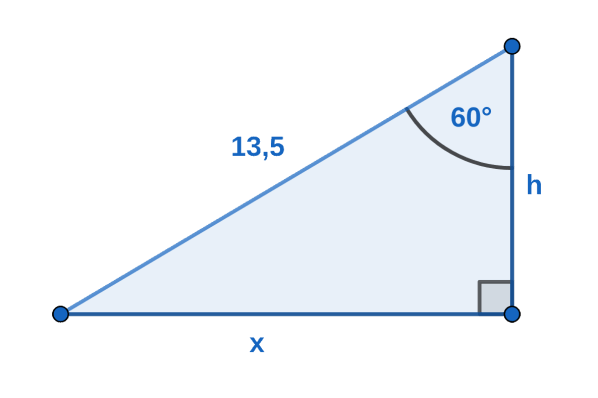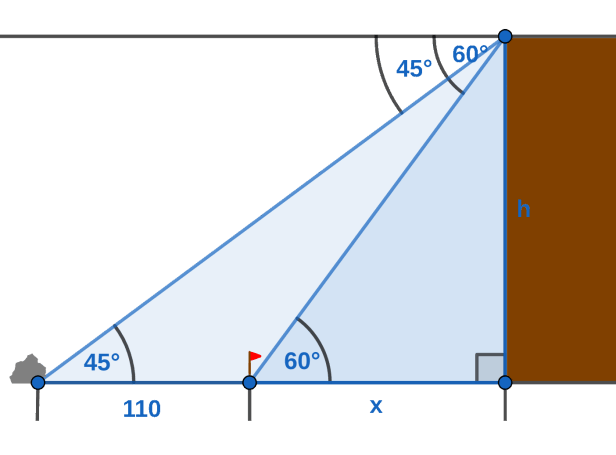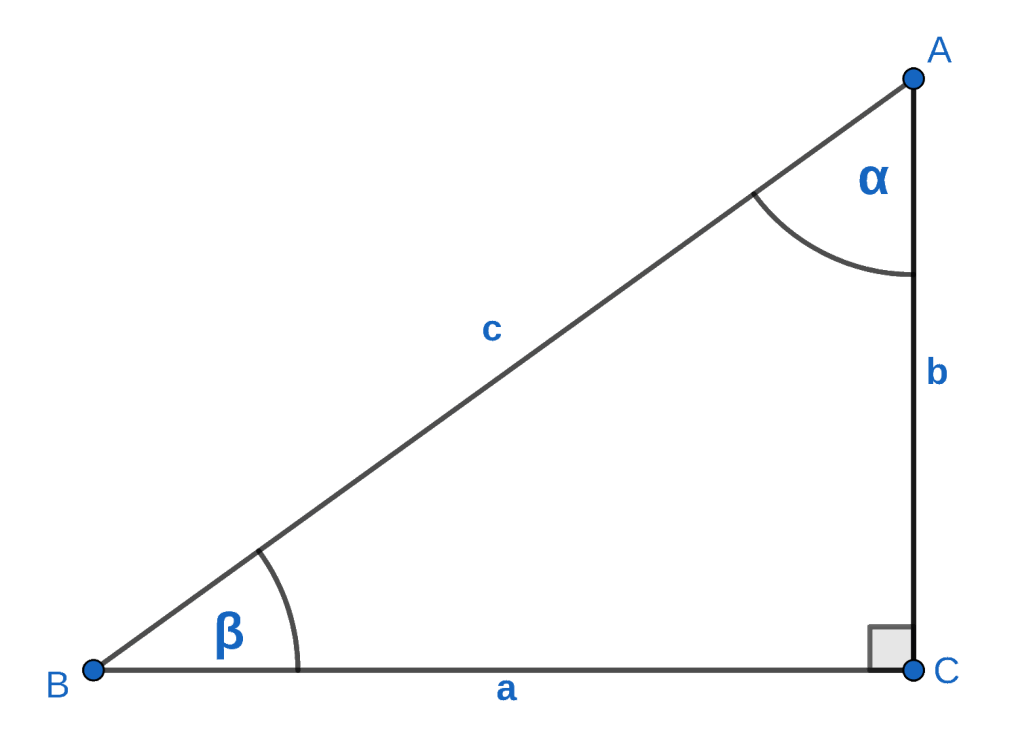
Seno: (cateto opuesto) / (hipotenusa)
sen α = a/c sen β = b/c
Coseno: (cateto adyacente) / (hipotenusa)
cos α = b/c cos β = a/c
Tangente: (cateto opuesto) / (cateto adyacente)
tan α = a/b tan β = b/a
Cotangente: (cateto adyacente) / (cateto opuesto)
cot α = b/a cot β = a/b
Secante: (hipotenusa) / (cateto adyacente)
sec α = c/b sec β = c/a
Cosecante: (hipotenusa) / (cateto opuesto)
csc α = c/a csc β = c/b
α=(π/4) --> β=(π/4)
Dado que el ΔABC es isósceles, se tiene a=b. Luego:
c2 = a2 + b2 --> c2 = 2a2
--> c=a√2
sen(π/4) = (√2)/2
cos(π/4) = (√2)/2
tan(π/4) = (√2)/2
¿Puedes encontrar los valores sec(π/4) , csc(π/4) , ctg(π/4)?
β=(π/3) --> α=(π/6)
Dado que el ΔABD es equilátero, trazaremos una altura desde A, que pasa por C. Con ello, se tiene a=(c/2). Luego:
c2 = a2 + b2 --> b2 = c2 - a2
--> b2 = c2 - (c/2)2
--> b2 = (3/4)c2
--> b = (√3/2)c
sen(π/6) = 1/2
cos(π/6) = (√3)/2
tan(π/6) = (√3)/3
¿Puedes encontrar los valores sec(π/6) , csc(π/6) , ctg(π/6)?
| Ángulo | 0 | π/6 | π/4 | π/3 | π/2 |
|---|---|---|---|---|---|
| sen | 0 | 1/2 | (√2)/2 | (√3)/2 | 1 |
| cos | 1 | (√3)/2 | (√2)/2 | 1/2 | 0 |
| tan | 0 | (√3)/3 | 1 | √3 | no existe |
| cot | no existe | √3 | 1 | √3/3 | 0 |
| sec | 1 | 2(√3)/3 | √2 | 2 | no existe |
| csc | no existe | 2 | √2 | 2√3/3 | 1 |
Ejemplo 1: Calcular el valor de la siguiente expresión:
E = sen3(π/3)cot(π/6) - sec2(π/4) + 3cos(π/3)tan(π/4) - tan2(π/3)
Solución: sen(π/3) = (√3)/2
cos(π/3) = 1/2
tan(π/3) = √3
tan(π/4) = 1
sec(π/4) = √2
cot(π/6) = √3
E = (3√3/8)x√3 - 2 + 3x(1/2)x1 - 3
E = 9/8 - 2 + (3/2) - 3
E = -(7/8) - 12/8
E = -19/8 .//
Ejemplo 2: Un triángulo rectángulo tiene por hipotenusa c = 8 m y además senα = 1/2. Determinar la medida de los catetos (a y b).
Solución: senα = 1/2 = a/8
--> a = 8/2 = 4 m
c2 = a2 + b2 --> b2 = c2 - a2
b2 = (8 m)2 - (4 m)2
b2 = (64 - 16) m2 = 48 m2
--> b = √48 m = 4√3 m
Finalmente, los catetos miden 4m y 4√3 m .//
Ejemplo 3: Si β es tal que 0<β<π/2 y tanβ = 1/2, determinar el valor de cosβ.
Solución: tanβ = 1/2 = b/a
--> 2b = a
c2 = a2 + b2 = (2b)2 + b2
= 4b2 + b2 = 5b2
--> c = b√5
cosβ = a/c = (2b)/(b√5)
= 2/(√5) = 2√5/5 .//
Ejemplo 4: Una colina mide 420 m de altura. Se sabe que el ángulo de elevación de la cima con respecto a un punto R en el suelo es de 30°. Determinar la distancia desde R al pie de la colina.
Solución: Un ángulo de elevación es un ángulo medido desde el suelo hacia arriba:
θ = 30° = π/6 --> tan(π/6) = √3/3
Como la altura del cerro es h = 420 m, se obtiene:
tan(π/6) = h/x = √3/3
--> x = 3h/√3 = h√3
--> x = 420√3 m .//
Ejemplo 5: Una escalera de 13,5 m de largo llega hasta el borde superior de un muro. Si la escalera forma un ángulo de 60° con el muro, hallar la altura del muro y la distancia en el suelo entre muro y escalera.
Solución: θ = 60° = π/3 --> tan(π/3) = √3 = x/h
--> x = h√3
--> (13,5 m)2 = x2 + h2
--> 182,25 m2 = (h√3)2 + h2
--> 182,25 m2 = 3h2 + h2
--> 4h2 = 182,25 m2
--> h2 = 45,5625 m2
--> h = 6,75 m
--> x = h√3 = 6,75√3 m = 11,69 m .//
Ejemplo 6: Mirando desde la parte superior de un acantilado, los ángulos de depresión de una roca y de una boya son 45° y 60° respectivamente. Si se sabe que hay 110 m entre la roca y la boya, hallar la altura del acantilado.
Solución: θ = 45° = π/4 --> tan(π/4) = 1 = h/(110+x)
--> h = 110+x --> x = h - 110
θ = 60° = π/3 --> tan(π/3) = √3 = h/x
--> x = h/√3 = h√3/3
--> h - 110 = h√3/3
--> 3h - 330 = h√3
--> (3-√3)h = 330
--> h = 330/(3-√3)
--> h = 260,3 m .//